Prove each of the following identities `(tan theta)/((1 tan^(2) theta)^(2)) (cot theta)/((1 cot^(2) theta)^(2)) = sin theta cos theta `Prove the Following Trigonometric Identities `Tan^2 Theta Sin^2 Theta Tan^2 Theta Sin^2 Theta` CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Question Bank Solutions 466 Concept Notes &Let's say that we're told that some angle theta which is going to be expressed in radians is between negative 3 PI over 2 and negative PI it's greater than negative 3 PI over 2 it's less than negative PI and we're also told that sine of theta is equal to 1/2 from just from this information can we figure out what the tangent of theta is going to be equal to and I encourage you to pause the

Trigonometric Identities Topics In Trigonometry
Tan 2 theta identities
Tan 2 theta identities-1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θIn trigonometrical ratios of angles (90° θ) we will find the relation between all six trigonometrical ratios Let a rotating line OA rotates about O in the anticlockwise direction, from initial position to ending position makes an angle ∠XOA = θ again the same rotating line rotates in the same direction and makes an angle ∠AOB =90°



Bestmaths Online Proof 4
Trigonometric Simplification Calculator \square!SUMMARIZING TRIGONOMETRIC IDENTITIES The Pythagorean identities are based on the properties of a right triangle (See Sections 63 and 64) cos 2 θ sin 2 θ = 1 1 cot 2 θ = csc 2 θ 1 tan 2 θ = sec 2 θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the$\tan^2{\theta} \,=\, \sec^2{\theta}1$ The square of tan function equals to the subtraction of one from the square of secant function is called the tan squared formula It is also called as the square of tan function identity Introduction The tangent functions are often involved in trigonometric expressions and equations in square form The
When solving some trigonometric equations, it becomes necessary to first rewrite the equation using trigonometric identities One of the most common is the Pythagorean Identity, \(\sin ^{2} (\theta )\cos ^{2} (\theta )=1\) which allows you to rewrite \(\sin ^{2} (\theta )\) in terms of \(\cos ^{2} (\theta )\) or vice versa,The subtraction of the tan squared of angle from secant squared of angle is equal to one and it is called as the Pythagorean identity of secant and tangent functions $\sec^2{\theta}\tan^2{\theta} \,=\, 1$ Popular forms The Pythagorean identity of secant and tan functions can also be written popularly in two other forms $\sec^2{x}\tan^2{x} \,=\, 1$ Prove each of the following identities `(1 tan theta cot theta )( sin theta cos theta ) =((sec theta)/("cosec"^(2) theta ) ("cosec"theta)/(se asked in Trigonometry by Ayush01 ( 447k points)
In trigonometry, tangent halfangle formulas relate the tangent of half of an angle to trigonometric functions of the entire angle The tangent of half an angle is the stereographic projection of the circle onto a line Among these formulas are the following tan 1 2 ( η ± θ ) = tan 1 2 η ± tan 1 2 θ 1 ∓ tan 1 2 η tan 1 2 θ = sin η ± sin θ cos η cos θ = − cos η − cos θ sin η ∓ Trigonometric Identities The distances or heights can be calculated using mathematical techniques that fall under the category of 'trigonometry' The word 'trigonometry' comes from the Greek words 'tri' (meaning three), 'gon' (meaning sides), and 'metron' (meaning measure) (meaning measure) Trigonometry, in reality, isPythagorean identities are identities in trigonometry that are extensions of the Pythagorean theorem The fundamental identity states that for any angle θ, \theta, θ, cos 2 θ sin 2 θ = 1 \cos^2\theta\sin^2\theta=1 cos2 θsin2 θ = 1 Pythagorean identities are useful in simplifying trigonometric expressions, especially in




Solved Does Tan 2 Theta Frac Sin 2 Theta Cos 2 Theta Justify Your Answer



Trigonometry Trigonometric Laws And Identities
Here is a summary for this final type of trig substitution √a2b2x2 ⇒ x = a b tanθ, −π 2 < θ < π 2 a 2 b 2 x 2 ⇒ x = a b tan θ, − π 2 < θ < π 2 Before proceeding with some more examples let's discuss just how we knew to use the substitutions thatGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!{eq}3 \sec^2 \theta 3 \tan^2 \theta {/eq} Trig Identities In this problem we want to use one of the fundamental trig identities to write the given expression as an integer




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco
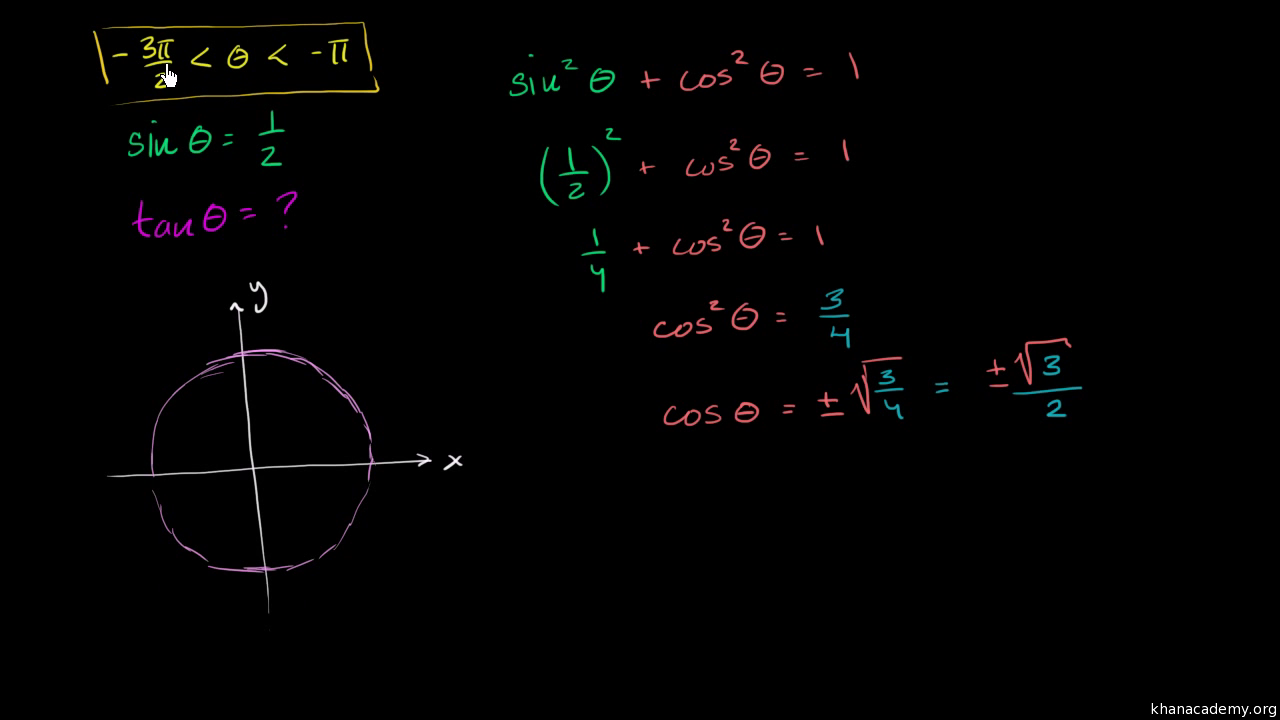



Using The Pythagorean Trig Identity Video Khan Academy
The expression is 1 tan2θ = 1 sin2θ cos2θ = cos2θ sin2θ cos2θ = 1 cos2θ = sec2θ Answer link Harish Chandra Rajpoot 1 tan2θ = sec2θ\(\displaystyle 3s 7s = 10s\)In an identity, the expressions on either side of the equal sign are equivalent expressions, because they have the same value for all values of the variable Identity An identity is an equation that is true for all legitimate values of the variables Example 541 Which of the following equations are identities?




How Do You Prove The Identity Sectheta Tantheta 2 1 Sintheta 1 Sintheta Homeworklib




How Do You Verify The Identity Tan2theta 2 Cottheta Tantheta Socratic
Trigonometric Identities ( Math Trig Identities) sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x) Trigonometric Identities Basic Definitions Definition of tangent $ \tan \theta = \frac{\sin \theta}{\cos\theta} $ Definition of cotangent $ \cot \theta = \frac{\cos Half Angle Formula Cosine Using a similar process, with the same substitution of `theta=alpha/2` (so 2θ = α) we subsitute into the identity cos 2θ = 2cos 2 θ − 1 (see cosine of a double angle) We obtain `cos alpha=2\ cos^2(alpha/2)1`



Trigonometry Identities



Trigonometric Identities And Equations Ppt Download
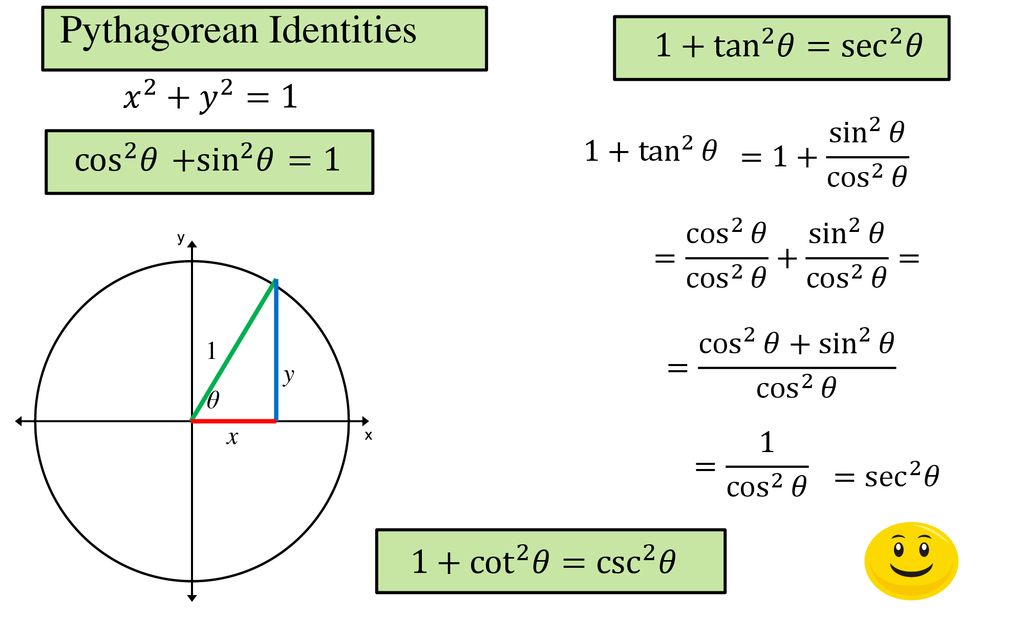
The Pythagorean Identities $$\begin{array}{c} \cos^2 \theta \sin^2 \theta = 1\\ 1 \tan^2 \theta = \sec^2 \theta\\ 1 \cot^2 \theta = \csc^2 \theta \end{array}$$ Even/Odd Function Identities $$\begin{array}{rcl} \cos (\theta) &=& \phantom{}\cos \theta\\ \sin (\theta) &=& \sin \theta\\ \tan (\theta) &=& \tan \theta \\ \end{array}$$Math2org Math Tables Trigonometric Identities sin (theta) = a / c csc (theta) = 1 / sin (theta) = c / a cos (theta) = b / c sec (theta) = 1 / cos (theta) = c / b tan (theta) = sin (theta) / cos (theta) = a / b cot (theta) = 1/ tan (theta) = b / a sin (x) = sin (x) Quotient and reciprocal identities Cofunction Function identities Even/Odd Functions Pythagorean identities Angle sum and difference identities Doubleangle identities Halfangle identitie s Reduction formulas



3




14 2 Trigonometric Identities
The three basic trig functions are the Sine, Cosine, and Tangent functions Let's begin by looking at the sine function In the context of a right angle, the sine function, written as $\sin{\theta}$ is equal to the division of the opposite side of the reference angle $(\theta)$ by the hypotenuse, or long side, of the triangle 9 sec 2 θ − 5 tan 2 θ Here use the Pythagorean trigonometry identity, tan 2 θ 1 = sec 2 θ 9 sec 2 θ − 5 tan 2 θ = 9 sec 2 θ − 5 ( sec 2 θ − 1) = 9 sec 2 θ − 5 sec 2 θ 5 = 5 4 sec 2 θ Therefore it is established that the lefthand side equal toFollowing table gives the double angle identities which can be used while solving the equations You can also have sin2θ,cos2θ expressed in terms of tanθ as under sin2θ = 2tanθ 1 tan2θ cos2θ = 1 −tan2θ 1 tan2θ sankarankalyanam 1



Bestmaths Online Proof 4



Show That None Of The Following Is An Identity Tan 2 8 Sin 8 Cos 2 8 Sarthaks Econnect Largest Online Education Community
Rewrite tan(θ) tan ( θ) in terms of sines and cosines Multiply by the reciprocal of the fraction to divide by 1 cos(θ) 1 cos ( θ) Write cos(θ) cos ( θ) as a fraction with denominator 1 1 Cancel the common factor of cos(θ) cos ( θ) 3 2 1 Steps For finding the values of sinθ 1) Write counting from 0 to 4 2) Divide all the numbers by 4 and simplify these numbers 3) Taking square root of all these numbers 4) The values we get are the values on the sin function at different standard angles For values of other trigonometric ratiosQuestion (tan Θ/1cot Θ)(cot Θ/1tan Θ) = 1sec Θcosec ΘBook NCERTChapter Trigonometric identitiesFollow on my social media for latest update _____And



31 35 Y 3 Sin 4x 36 40 Y Cos X 41 45 Y 5 Tan 2x Gauthmath




Cos Squared Theta Minus Sin Square Theta Equal To 1 Minus 10 Squared Theta By 1 10 Squared Theta Prove The Identity Class Of Achievers
Tan 2 θ = 2 tan x 1 − tan 2 x \tan 2 \theta = {{2\tan x} \over {1 \tan ^2}x} tan 2 θ = 1 − t a n 2 x 2 t a n x 1 Express each of the following in terms of a single trigonometric functionThe second shows how we can express cos θ in terms of sin θ Note sin 2 θ "sine squared theta" means (sin θ) 2 Problem 3 A 345 triangle is rightangled a) Why?Instead, think that the tangent of an angle in the unit circle is the slope If you pick a point on the circle then the slope will be its y coordinate over its x coordinate, ie y/x So at point (1, 0) at 0° then the tan = y/x = 0/1 = 0 At 45° or pi/4, we are at an x, y of (√2/2, √2/2) and y / x for those weird numbers is 1 so tan 45




Prove The Identity Sec 4 Theta Sec 2 Theta Tan 4 Theta Tan 2 Theta




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
θ 1) = tan 2 θ Start with the lefthand side of the given identity as LHS= (secθ−1)(secθ1) L H S = ( sec θ − 1) ( sec θ 1) Apply the algebraic formula (a−b You can either expand or simplify the triple angle tan functions like tan 3 A, tan 3 x, tan 3 alpha etc by using triple angle identity Tan 3 theta = 3 tan theta – tan 3 theta / 1 – 3 tan 2 theta Where tan is a tangent function and theta is an angle This is one of the important trigonometry formulas Tan 3x Formula Example Trigonometry Formulas As a lot of the Earth's natural structures resemble triangles, Trigonometry is a very important part of Mathematics during high schoolIt is used across different areas of work such as engineering architecture, and different scientific specializations However, Trigonometry requires students to memorise different formulas of sin, cos, tan, sec, cosec, and




Answered If X 2 Tan Theta Write The Expression Bartleby



If Cos Theta 8 17 And Theta Is In Quadrant 3 What Is Cos2 Theta And Tan2 Theta Brainly Com
In this video, we will prove the identity square of tangent of theta 1 = square of secant of thetaOther topics for the videoProof of the identity 1 tanAll the trigonometric identities on one page Color coded Mobile friendly With PDF and JPG downloads Trig Identities Download PDF Download JPG Reciprocal Identities I highly recommend this 3minute $$ \tan(2\theta) = \frac{2\tan\theta}{1\tan^2\theta} $$Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Trigonometry Trigonometric Laws And Identities




Show That The Following Are Not Trigonometric Identities 1 Tan 2x 2tan X 2 Sec X Sqrt 1 Tan 2 X 3 Sin X Y Sin X Sin Y Study Com
The two identities labeled a') "aprime" are simply different versions of a) The first shows how we can express sin θ in terms of cos θ;Trigonometric Equation Calculator \square!




Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1




What Is The Integration Of Tan 2x Solution Quora




Trigonometric Identities A Plus Topper




Prove That 1 Tan Theta Tan 2theta Sec 2theta Youtube




Summary Of Trigonometric Identities




Trigonometric Identities Topics In Trigonometry




Summary Of Trigonometric Identities



1




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x



What Is The Formula Of Tan2x Quora



Ilectureonline




Tangent Half Angle Formula Wikipedia




Trigonometric Identities Simplify Expressions Video Lessons Examples And Solutions
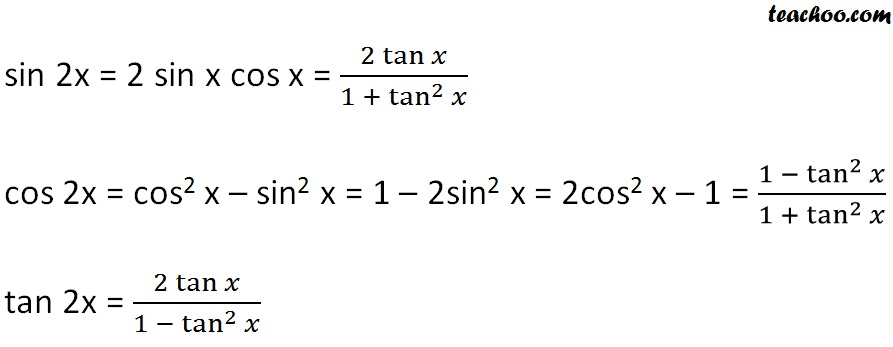



Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi




Trigonometric Identities Sin 2 X Cos 2 X Tan 2 X Youtube



Which Of The Following Is A Trigonometric Identity A Cot Theta Tan Theta 1b Brainly Com



How I Remember Trig Identities Part 2 Beyond Solutions




If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2 Theta




Prove The Following Trigonometric Identities 1 Cot 2theta 1 Costheta 1 Costheta 1 Ii Tan 2theta 1 Cos 2theta 1




Lista Over Trigonometriska Identiteter Wikipedia




Cos Theta Tan Theta 2 2tan Theta 1 2 Sec Theta 5 Sin Theta Youtube




What Does Tan 2 Theta Equal




Prove Sec 2 Theta 1 Tan 2 Theta




Prove The Identity Sin 2 Theta 2 Tan Theta Sin Theta 2tan Theta Study Com




5 1 Fundamental Trig Identities Reciprocal Identities Sin



Complex And Trigonometric Identities Introduction To Digital Filters



What Is Tan 2 Theta Equal To




Tangent Half Angle Formula Wikipedia



Prove Tan 2 8 Sin 2 8 Tan 2 8 Sin 2 8 Sarthaks Econnect Largest Online Education Community



If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora




18 17 Prove That Cot 2 A Csc 2



If Tan 2theta 1 2tan 2a T Mathematics Topperlearning Com 47




Proof Tan 2 1 Sec 2 Youtube
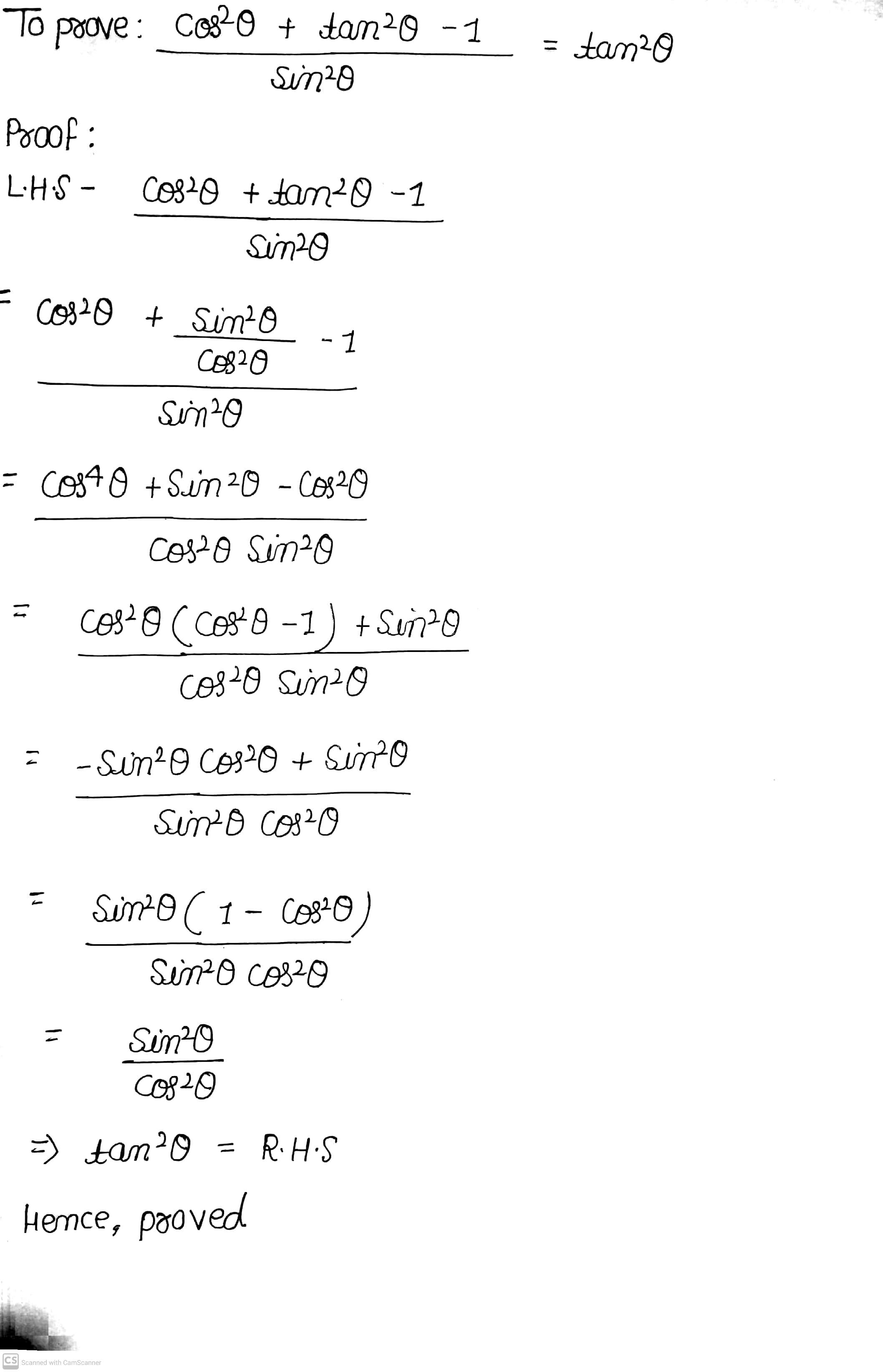



9 Prove The Identity Tex Frac Cos 2 Theta Tan 2 Theta 1 Sin 2 Theta Tan 2 Theta Tex 16 56sbfrc Dgxwyzf Snapsolve




Solved Verify The Following Identity 2 Tan 8 Sin 1 Tan 2 Chegg Com




最も人気のある Tan2 Identity ただの悪魔の画像



Cochranmath Solving Trigonometric Equations
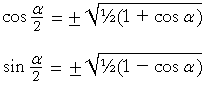



Trigonometric Identities Topics In Trigonometry




Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf
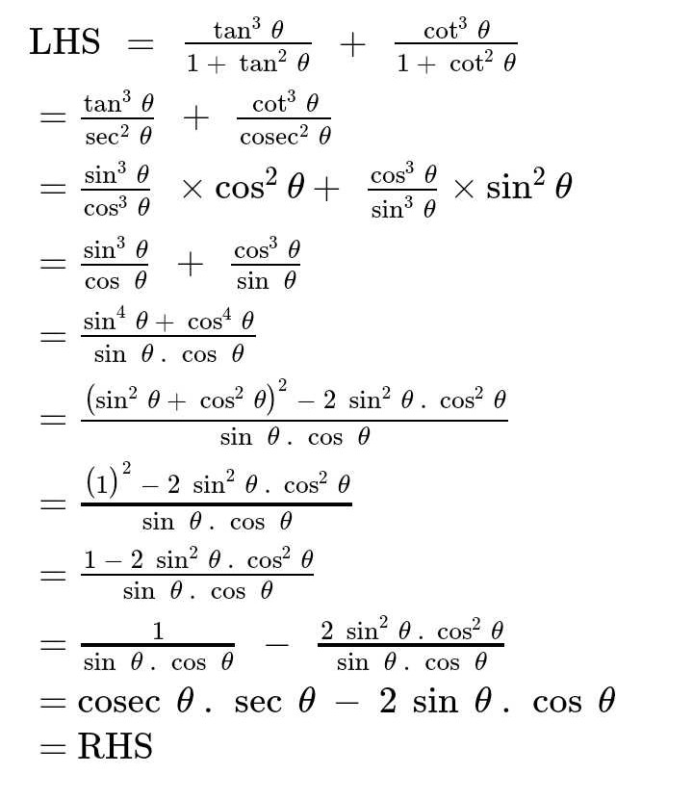



Prove If Tan 3 Theta 1 Tan 2 Theta Cot 3 Theta 1 Cot 2 Theta Sec Theta Cosec Theta 2 Sin Theta Cos Theta Edurev Class 10 Question



Solving Trigonometric Equations With Identities Algebra And Trigonometry




Sin Theta Cos Theta 1 Sin Theta Cos Theta 1 1 Sec Theta Tan Theta Using The Identity Sen Theta 1 Tan Theta Maths Introduction To Trigonometry Meritnation Com



The Trigonometric Ratios Of Angl



3



Ilectureonline




Tangent Half Angle Formula Wikipedia




Integrate Tan 2x




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



1
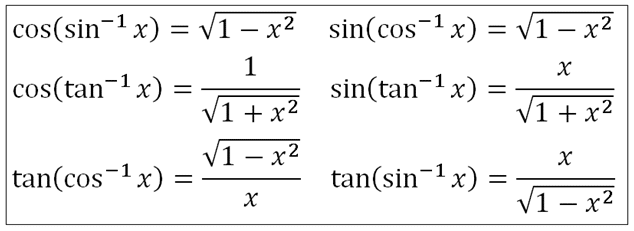



Inverse Trig Identities Reciprocal Of Trigonometric Function Trig




How To Use Double Angle Identities Studypug




Art Of Problem Solving




上 Tan2x Identity ただの悪魔の画像
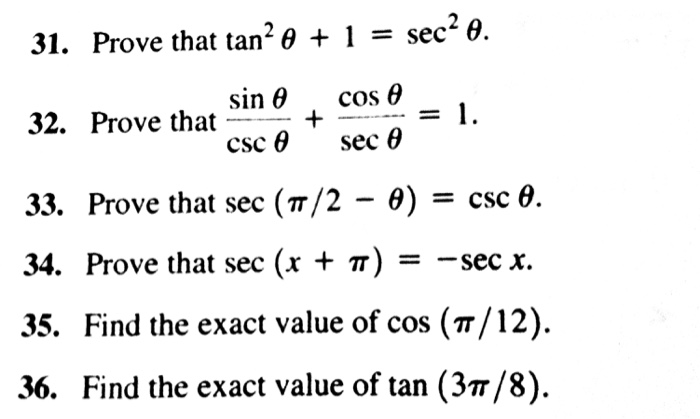



Solved 31 Prove That Tan 2 Theta 1 Sec 2 Theta 32 Chegg Com
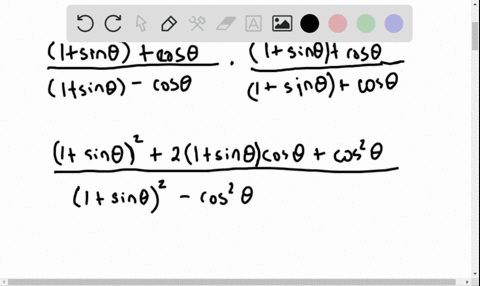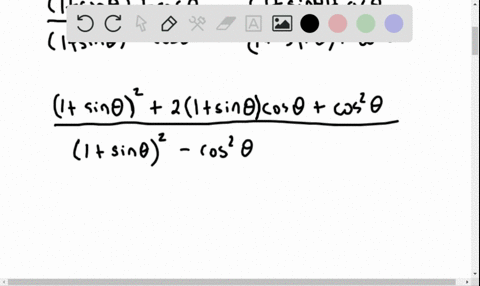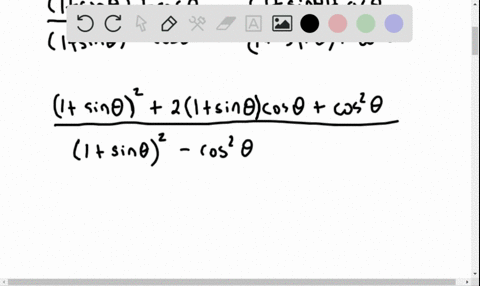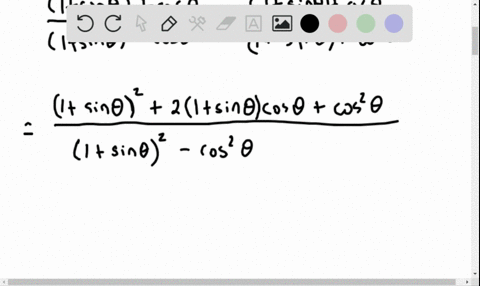



Solved Establish Each Identity Frac 1 2 Cos 2 Theta Sin Theta Cos Theta Tan Theta Cot Theta




Trigonometric Identities With Pdf Download Math Tutor




14 2 Trigonometric Identities




5 1 5 2 Trigonometric Identities Ppt Download




Trigonometric Identity Review Trigonometry Identities Reciprocal Identities Sin 8 Cos 8 Tan 8 Quotient Identities Tan 8 Cot 8 Ppt Download




Integrate Cosec 2x




Precalculus Trigonometry Trig Identities 29 Of 57 Formula For Lowering Power Tan 2 X Youtube




Trigonometric Identities With Pdf Download Math Tutor




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download
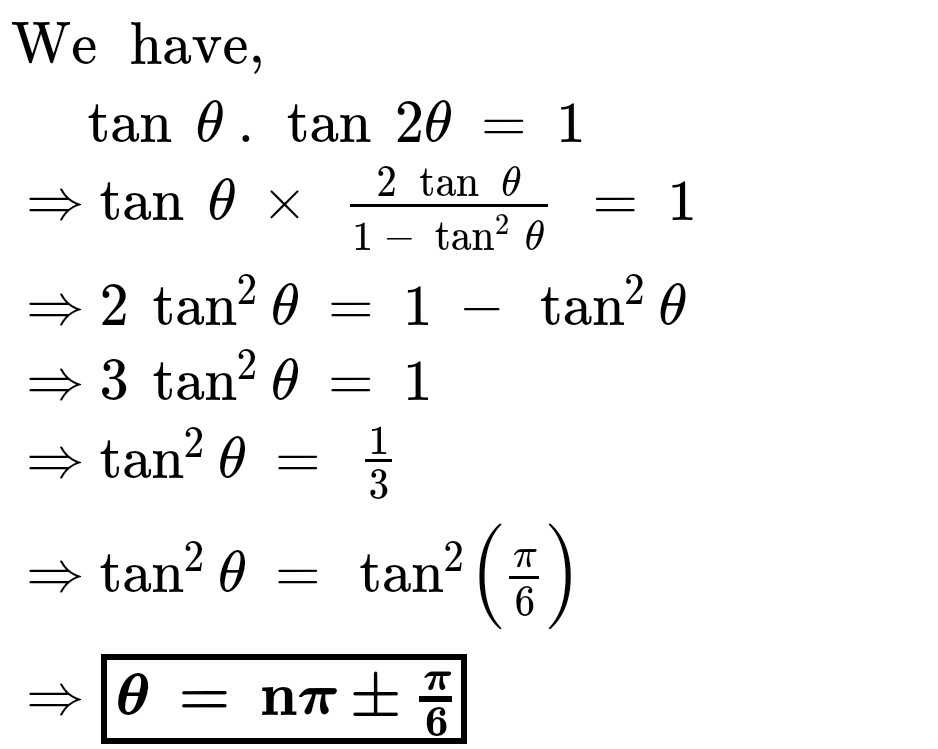



The No If Solution Of The Equation Tan 2theta Tan Theta 1 Scholr




Summary Of Trigonometric Identities
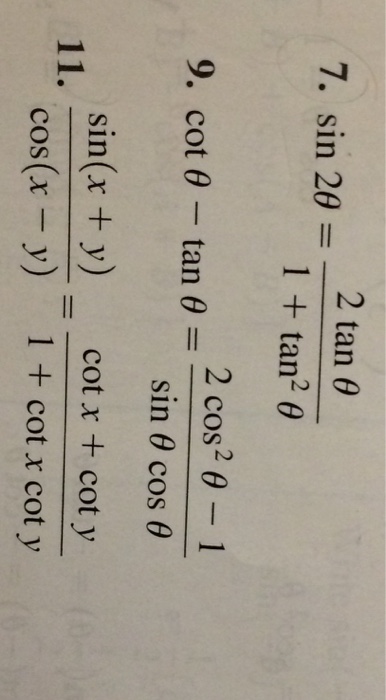



Solved Sin 2 Theta 2 Tan Theta 1 Tan 2 Theta Cot Theta Chegg Com




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




bestpictjcry Tan 2x Tan 2x
x-1=sec(squared)x.jpg)



10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com




Omtex Classes Prove The Identity Sin8 Cosec8 2 Cosec8 Sec8 2 7 Tan 2 8 Cot 2 8
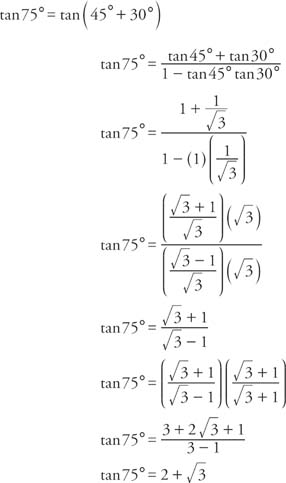



Tangent Identities




3 7 Trigonometric Identities Precalculus



Cbse 10 Math Cbse Introduction To Trigonometry Ncert Solutions
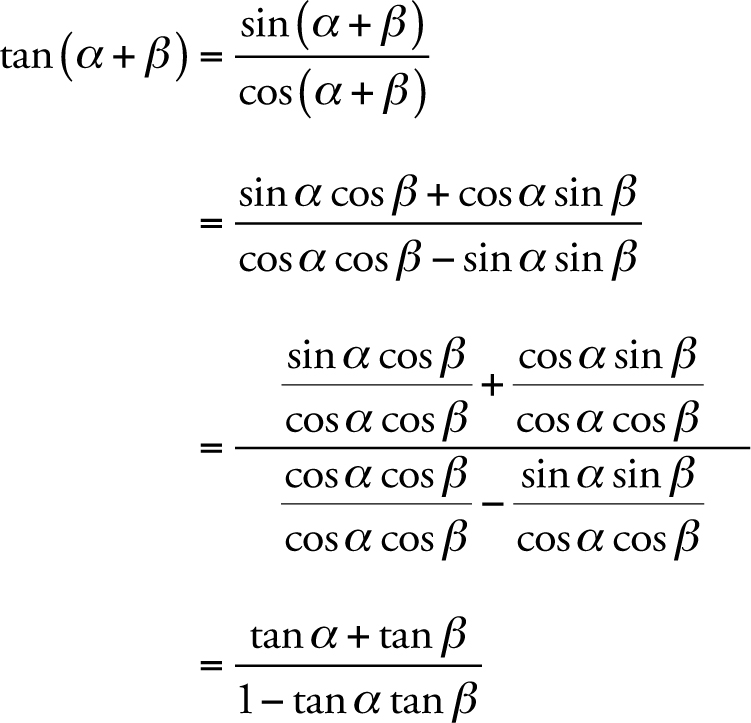



Tangent Identities




Trigonometric Identities A Plus Topper




Double Angle Formulas Trigonometry Teachoo 2x 3x Formula Provi



Prove The Following Identities Sin 4 8 Cos 4 8 Gauthmath
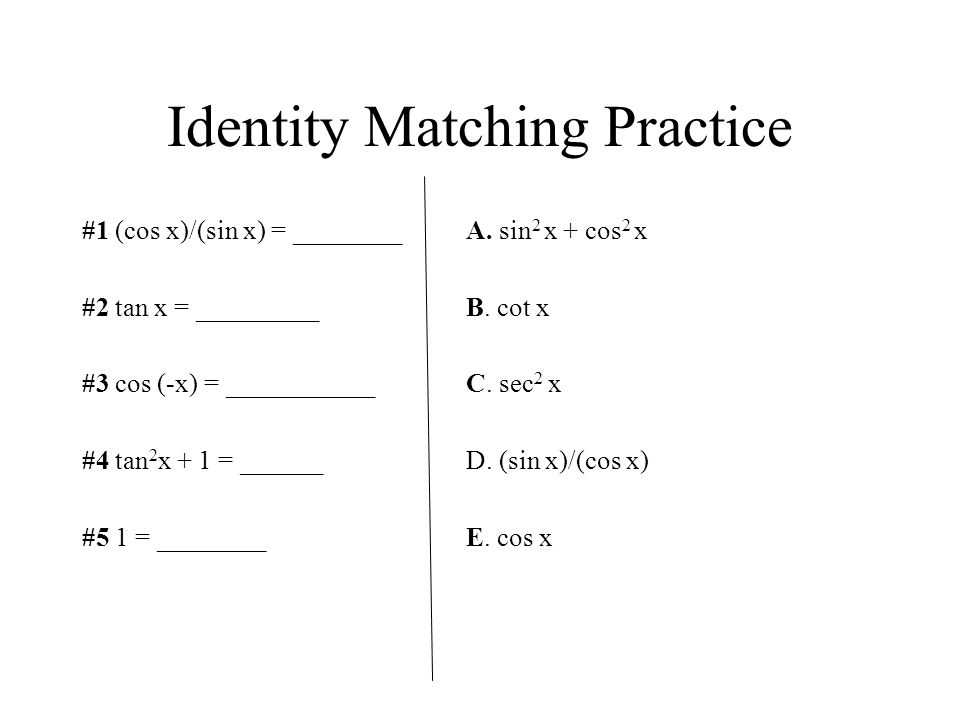



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download




Prove The Following Identity From Mathematics Introduction To Trigonometry Class 10 Cbse
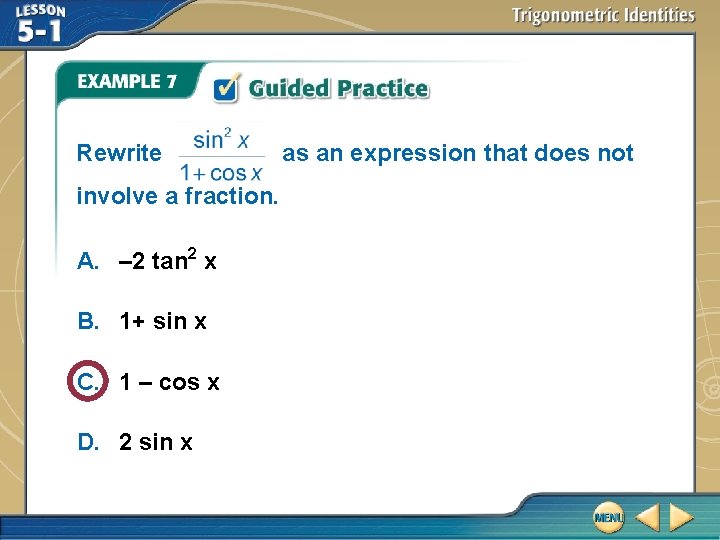



Lesson 5 1 Trigonometric Identities Fiveminute Check Over
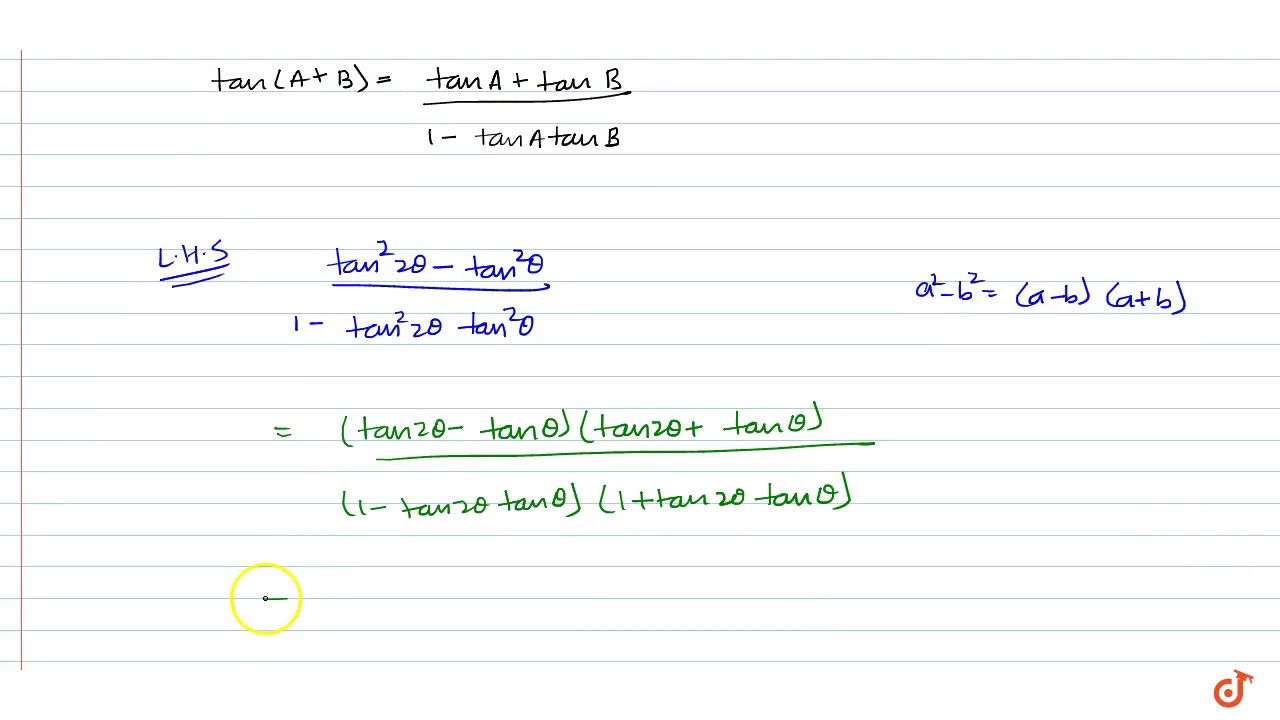



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube




Solved Prove That Tan 2theta Sec Theta 1 2 1 Cos Theta 1



2




Trigonometric Identities



0 件のコメント:
コメントを投稿